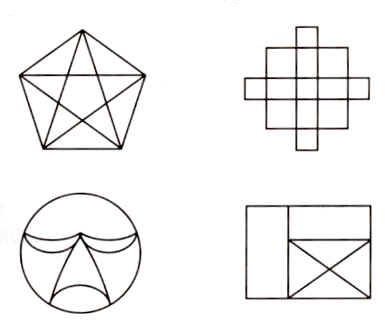
一筆畫圖形是歷久不衰的數學難題,就如上圖所示的4個圖形可以一筆完成嗎?如果每次看到圖形都感到眼花繚亂,或許這個一筆畫圖形的秘密能幫助你!
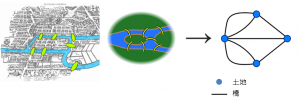
一筆畫圖形其實是源於十八世紀一個七橋難題,當時的哥尼斯堡 (今俄羅斯加里寧格勒) 有七條橋連接普列戈利亞河的兩岸,而城中的人每天都在看著名的哲學家康德在那裡散步。有人提出了一個疑問:「康德的散步路線能否經過所有橋卻不重覆呢?」於是人們不斷嘗試,雖然一直沒有找到答案,卻引起了數學家歐拉 (Euler) 的關注。他於1735年解開這個謎團,更在第二年發表了論文提出解決一筆畫問題。
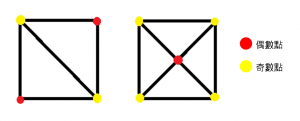
他以圖形來解決這個疑團。先將每塊土地以點來代替,再將每條橋以線來代替,得到以上 (最右) 圖形,然後就要看每個連接點上有多少條線連接上。例如A連接點上有3條線 (單數) 連上,所以這是一個奇數點,而B連接點上有5條線 (單數) 連上,也是一個奇數點。相反,如果連接點上的線條數目是雙數,就是一個偶數點。先來個練習吧!
當連接點都分類好,剩下的就是數一數奇數點的數目。如果圖形沒有奇數點,在任何一個點開始都能一筆後回到起點;如果圖形只有兩個奇數點,從其中一個奇數點開始也可以一筆繞過所有線後回到另一個奇數點。這些路線都稱為「歐拉迴路」,而其他情況的圖形都不能以一筆完成整幅畫。回到剛才七橋問題,由於4個連接點都屬於奇數點,所以我們沒法在不重覆的情況下走完所有橋了。
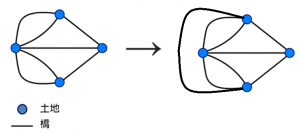
不過,當年政府為了方便市民可以不重覆地在兩岸散步,在1875年興建了第八座橋,把A及C連接點連起來 (如下圖)。這個改動使A及C連接點由奇數點變為偶數點,使整個圖形只有2個奇數點,這樣市民就可以在不重覆的情況下走過所有橋了。但後來那些橋因戰爭而被炸毀了,重建後橋的位置和數量都不同,所以我們只能在腦海中走完這條「歐拉迴路」了。
資料來源:
朴炅美(2004)。無所不在的數學現象(王海娟譯)。
https://zh.wikipedia.org/…/%E6%9F%AF%E5%B0%BC%E6%96%AF%E5%A…